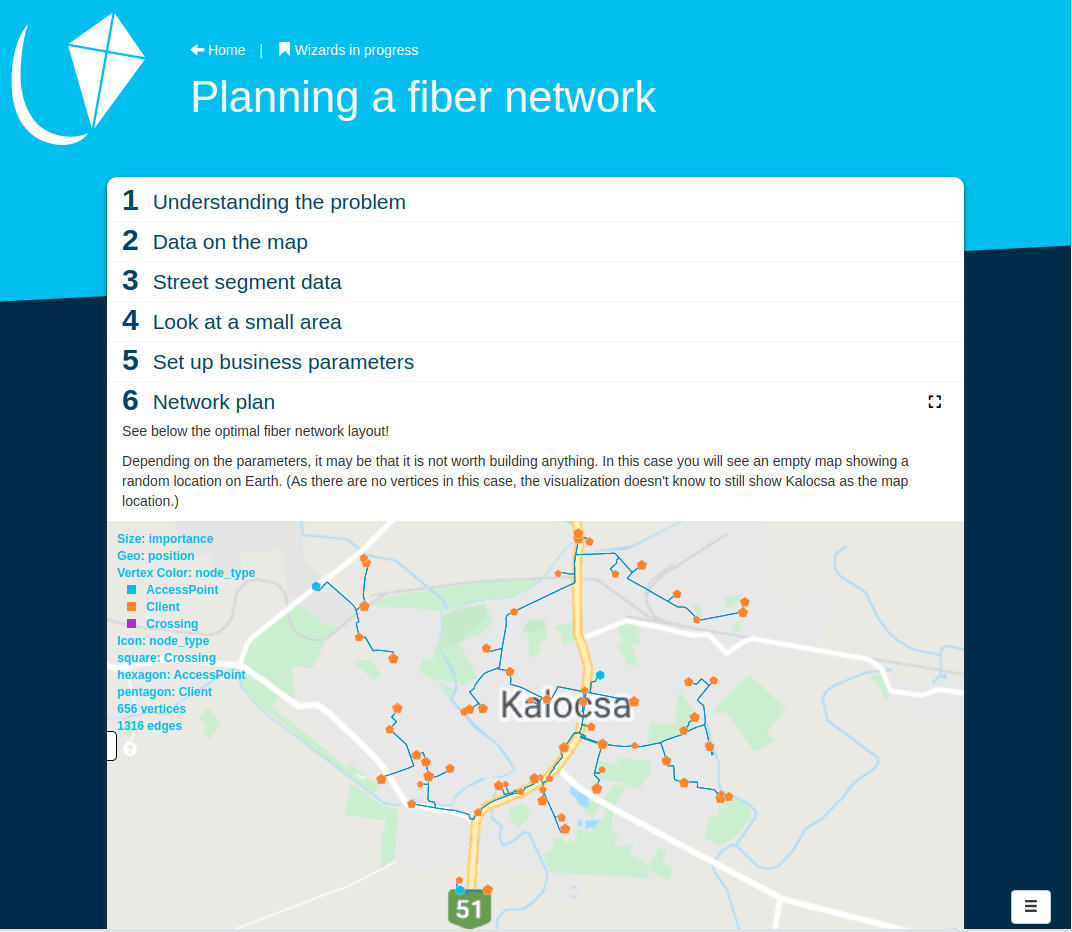
Designing a fiber network using LynxKite
Imagine you are an ISP, contemplating to set up shop in Kalocsa, the small but pretty town in the south of Hungary.
You are a pro, so you know the rules of the game all too well. You can lay fiber cables along streets. There is high bandwith internet already available for wholesale at a few locations in the town, at the so called Access Points or APs. Of course, connecting to an AP is not for free, and also laying cable is expensive, but you have pretty good ballpark numbers for the costs. Also, based on some market research, you have a pretty good idea of your potential customers. First you plan to cater for certain companies who are willing to pay a premium to have access to super fast Internet connection. You have these companies marked on a map together with the expected revenue you can hope to achieve from each.
So is it worth going there? Which AP (or APs) should you start your network from? Which clients to connect and which to skip for now? Where to lay the cables exactly?
LynxKite is able to help answering all the above questions!
The heart of the solution is the Find Steiner tree LynxKite operation.
More precisely, it helps solving an instance of a directed prize collecting
Steiner tree problem.
Say what?
This is a bit abstract, but widely applicable graph optimization problem. We are
given a directed graph with two vertex attributes (Root cost and Reward) and
one edge attribute (Cost). Root cost and Reward may only be defined on a subset of vertices.
A solution is a subgraph with certain vertices of it
marked as roots. A solution is valid, if all marked roots are potential roots (that is, with Root cost defined on them) in
the original graph and all vertices of the subgraph are accessible from a marked
root via a directed path in the subgraph.
For example, here is an instance of a price collecting Steiner tree problem:
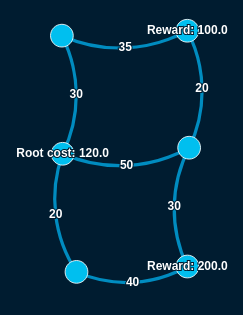
And this is the optimal solution:

The value of a solution is the sum of Rewards on all included vertices minus
all the costs. The costs are the sum of Root costs on the marked roots plus the
sum of Costs on all included edges. The value of the above example is 80.
So, basically, we want to reap as much reward as possible, with as little cost as possible. Story of our lives, eh?
The job of the Find Steiner tree operation is to find a solution with as much value
as possible. It is worth noting that finding the optimal solution is NP-complete,
so we can’t hope for the best possible solution in any possible instance of this
problem. But LynxKite depends on a
very advanced optimization algorithm
and tends to find the optimum in most practical cases in this class
of Steiner tree problems.
Observe that this abstract problem maps exactly to our concrete business
questions! We just use the map of Kalocsa as our original graph. We use the cost
of laying cables on a street segment as the Cost attribute.
The expected client revenues will play the role of Rewards. Finally, we set
Root cost on APs to the cost of connecting to the AP there. The value of a
solution is the profit of the corresponding buildout.
If you are interested in the details, head over to our cloud demo and take a look at the LynxKite workspace implementing all the steps of this analysis.
The analysis contains a number of business parameters. How much does it cost to lay a meter of fiber cable? What is the cost of APs? What discounting ratio we want to use when computing the net present value of the project?
The normal worflow would be that the data scientist preparing the analysis would provide a number of reports for certain combination of these business assumptions. Probably in an iterative process, business stakeholders asking new questions while the data scientist generates new reports.
How nice would it be if the business stakeholders could play around with these parameters themselves without having to understand the details of the analysis!
This is exactly what a LynxKite wizard is for! You can turn any LynxKite workspace for less technical users into a wizard by selecting certain parameters and outcomes to be exposed. Check out the above workspace turned into a magical being!
And if you are more into creating wizards than using them, check the anchor box on the above linked workspace to see how simple it was to create this wizard!